 |
|||||
|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
Method of Estimating Modulation Transfer Function (MTF) during development of the optical system comprising Objective, Photo Detector, and Image Processor.
Introduction.
Any device for registration of the video information consists of the following main components (subsystems):
- Objective;
- Photo detector;
- Image processor.
Since each of these subsystems contributes to the resulting resolution of the system it is possible to estimate MTF of the system using the product of MTF of the two main elements (the objective and the matrix of photo detectors) and by factoring in the influence of the digital image processing, which is usually implemented to correct the MTF of the system.
This paper describes such methodology of the complete photo/video system MTF estimation.
1. The estimation of the photo detectors matrix MTF.
1.1. Calculation of the frequency resolution limit for the given photo detector matrix.
Each matrix of photo detectors could be matched with the spatial frequency pass band. The limiting frequency for this pass band is Nyquist frequency defined by the Nyquist–Shannon sampling theorem. According to this theorem the exact reconstruction of a continuous-time baseband signal from its samples is possible if the signal is band limited and the sampling frequency is greater than twice the signal bandwidth. The sampling theorem was implied by the work of Harry Nyquist in 1928 ("Certain topics in telegraph transmission theory").
Therefore any CCD matrix is the spatial frequency filter. The parameters of this filter could be estimated using Fourier transform.
If used matrix has the pixel size or pixel pitch 
, the amount of pixel per millimeter will be:
.
From the above equation Nyquist frequency is defined as:
Modeling pass band of the sensor matrix demand modeling the change of the sensor matrix illumination level from black level to white level and, considering pixel pitch executing the Fourier transform
is the differentiation by subtracting the adjacent dots luminance values/
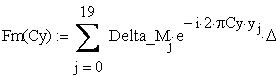
is the Fourier transform.
|
Where 
is the ideal normalized MTF of the photo detectors matrix.
Also in this case only 20 dots were considered for the estimation/
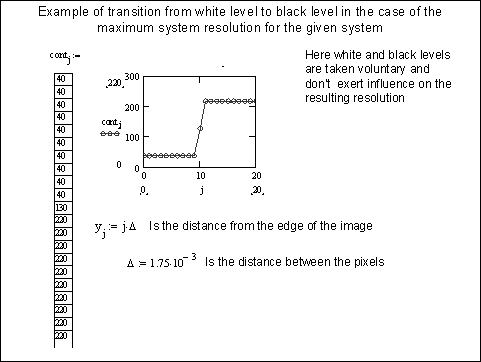
Fig 1. The response model of the ideal matrix.
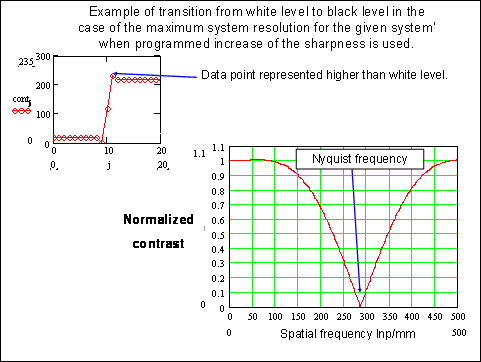
Fig. 2. MTF of the investigated sensor matrix.
1.2. The possibility of the sensor matrix MTF correction with the help of digital signal processing.
While using the CCD sensors we get the digital data as the output of the sensor. This allows the digital image to be enhanced with specially developed software. Such software detects the contrast edges and changes the luminance values of the dots on the edges as is shown in Figure 3.
This kind of digital image processing can not make the resolution of the system greater but distinctly enhance the image quality raising the mid frequency values of the MTF. That means that digital image processing may significantly increase the level of MTF for the contrast 0.5.
However sometimes this type of image enhancement may have negative impact on the overall image quality. To compensate for this, such parameter of the system as “sharpness” can be switched on and off with the help of corresponding software or, more often, system may be adjusted to the different levels of sharpness. In the following steps however the “sharpness” will not be considered because it has only auxiliary function in the combination of sensor and the objective.
Besides that, usually, there is the anti aliasing filter as a part of image processor, which suppresses all frequencies higher than Nyquist. Very often there is no need for such filtering because objective may fulfill the same function if its resolution is comparable to the sensor resolution.
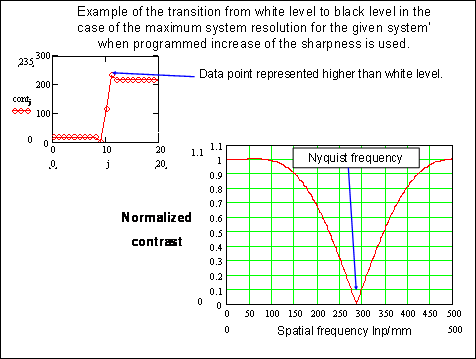
Fig. 3. Example of the digital image enhancement.
2. The estimation of the required objective MTF.
The resulting MTF is greatly influenced by the two components – objective and sensor matrix.
At the heart of the contemporary image quality analysis lays the concept of the image produced as a dual Fourier transform. The object and its image are represented as two dimensional distributions of the light intensity.
If the objective is drawing the image of some object, the latter is transformed from the linear structure to the spectrum of spatial frequencies which is getting passed through the frequency filter. This spectrum then again is transformed to the linear structure and becomes the light intensity variation of the image.
So the objective in this way is represented as a filter defining lower spatial frequency. The curve describing this filter is called Optical Transfer Function (OTF). Normalized to the zero frequency absolute value of this function is previously mentioned MTF.
The image of the dot produced with objective is called Point Spread Function (PSF). PSF is one of the main parameters describing the quality of the lens, but it is inconvenient for use when continuously distributed illumination is analyzed. Mathematically OTF and PSF may be derived from each other with the Fourier transform.
Figure 4 represents PSF of the ideal objective analytically calculated with Bessel function of the first kind.
In this article the sharp transition of luminance from the black level to the white level is investigated. Differentiating this transition leads to Line Spread Function (LSF) and the following execution of Fourier transform produces the MTF of the given system. LSF is more convenient for testing because it allows to use one dimensional calculation instead of two dimensional but for the circular aperture does not give the exact results.
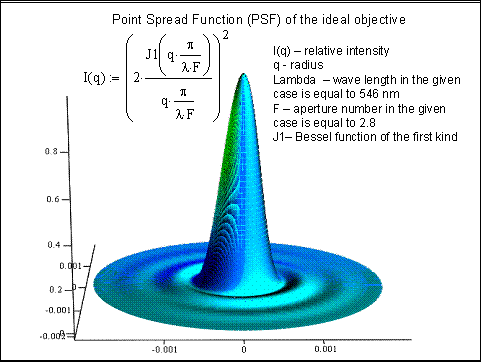
Fig. 4. PSF of the ideal objective.
The main input in resulting MTF is produced by the two important elements - objective and CCD matrix.
Diffraction limit of resolution of the ideal objective may be derived from the Sparrow criterion or the Rayleigh criterion and it depends on the wavelength of light.
Rayleigh criterion
Sparrow criterion
In these formulae F is the aperture number.
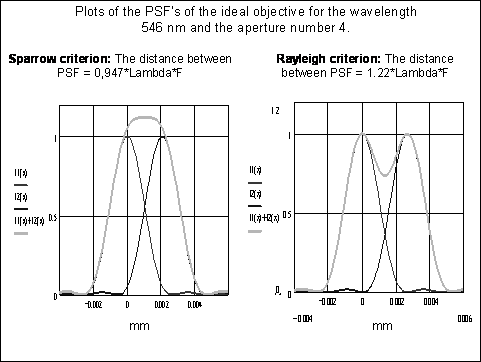
Fig. 5. Diagrams explaining Sparrow criterion and Rayleigh criterion.
MTF of the ideal objective is approximated using formula:
Where:
- MTF of the ideal objective;
Cy – spatial frequency;
DLln_mm - Diffraction limit of resolution of the ideal objective.
The Figure 6 represents functional relation of the ideal objective diffraction limit based on Rayleigh criterion and F number.
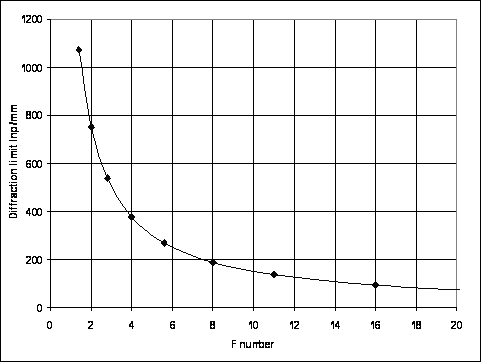
Fig. 6. The plot of the ideal objective diffraction limit VS F number.
The MTF of ideal objective for different F numbers is shown in Figure 7.
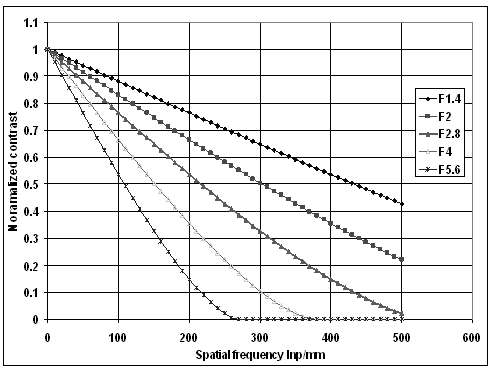
Fig. 7. The plot of the ideal objective MTF VS for different F number based on Rayleigh criterion.
However the use of Rayleigh criterion is not appropriate since according to it the contrast is not equal zero for the resolution limit though, considering the eye perception, for the telescope it is giving the correct number. For estimation of optical system MTF Sparrow criterion should be used.
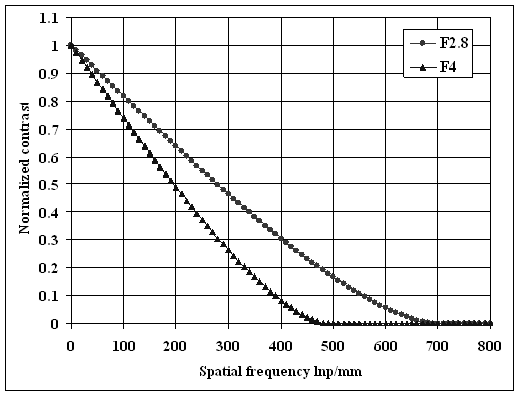
Fig. 8. MTF of the ideal objective with different F numbers based on Sparrow criterion.
3. Estimation of the system resolution using its estimated MTF.
To build the MTF of the system it is necessary to multiply the objective’s MTF ant the sensor matrix MTF. Figures 9 and 10 represent the results of such multiplication for the CCD with the pixel pitch 1.75 um and the ideal objective with the aperture number 2.8 or 4.
As it is seen from this figure the maximum possible F number is 4. However, it is impossible to avoid aberrations in the real lens, thus the F number should be at least 2.8. Under these circumstances the contrast 0.5 MTF point is less, than 136 lnp/mm and the MTF of the objective in this case at the same point is approximately equal 220 lnp/mm.
Obviously the actual objective built is going to have worse MTF and the analytical approximations would be worse too.
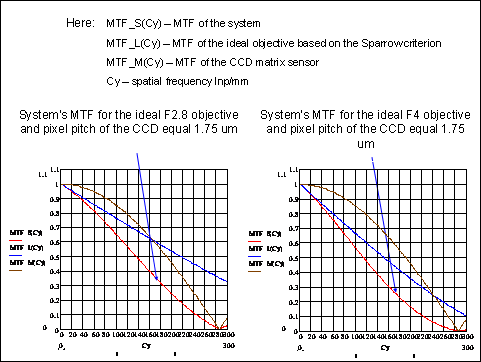
Fig. 9. Building the MTF of the system by multiplication of the objective and the sensor matrix MTF.
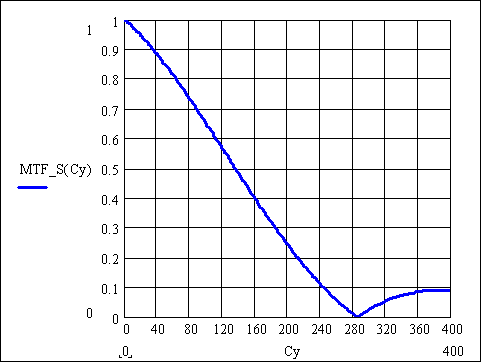я
Fig. 10. MTF of the ideal optical system consisting of the CCD matrix with the 1.75 um pixel pitch and the ideal objective with the 2.8 aperture number calculated with MathCAD software.
Reference Material
1. H. Nyquist, "Certain topics in telegraph transmission theory," Trans. AIEE, vol. 47, pp. 617—644, Apr. 1928
2. Robert R. Shannon, James C. Wyant, “Applied Optics and Optical Engineering”.
3. www.synopsys.com
4. www.mathsoft.com
